Heat Transfer in Fibrous Insulations
| Heat insulation is the process of blocking transfer of thermal energy between objects at different temperatures. Heat transfer occurs due conduction, convection, or radiation as well as any combination of these three mechanisms. Conduction can be reduced by eliminating the physical contact between the objects. Convection can be suppressed by suppressing the fluid motion (via friction, for instance), and radiation can be minimized by minimizing the view factor between the surfaces. Fibrous insulations can completely eradicate convective mode of heat transfer (thanks to the significant friction that their constituent fibers create against fluid flow) and also reduce the conductive and radiative modes to some extent.
Conductive heat in a fibrous material travels through both the air (interstitial fluid) and the fibers (solid phase). Generating 3-D geometries that resemble the microstructure of a fibrous materials, we studied the effective thermal conductivity of fibrous insulations having different microstructural properties. |
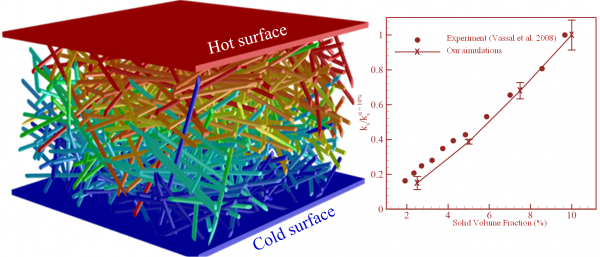 Our results indicate that heat conduction through the solid fibers increases by increasing fibers’ through-plane orientations (among others). The in-plane orientation of the fibers, on the other hand, did not show any influence on material’s conductivity. It was also shown that the microstructural parameters of fibrous insulations have negligible influence on the material’s performance if the conductivity of the solid phase is close to that of the interstitial fluid [Arambakam et al., 2013]. |
| Radiative heat transfer through fibrous insulation materials is often estimated using the Radiative transfer equation (RTE) which is a complicated integro-differential equation. Solving the RTE may need Monte Carlo Ray Tracing (MCRT), experiment, or analytical calculations to obtain the radiative characteristics (e.g., scattering phase function) of the media. Different approaches are considered for these calculations. The most popular approach is to first determine these properties for each individual fiber analytically, using for instance the Electromagnetic wave theory (e.g., Mie theory), and to then generalize the results to the whole media (see the next paragraphs). MCRT has also been used to estimate the radiative properties of fibrous insulation media or to directly calculate the temperature or heat flux in a system in the absence of a continuum phase (i.e., the air entrapped between the fibers). The general procedure in MCRT is to emit a large number of energy bundles from random positions and directions from a given surface, and then trace their propagation through the media until they exit the domain or become absorbed by the fibers. Parameters needed for MCRT in fibrous media include the basic microstructural parameters of the material such as fiber diameter, fiber optical properties, material porosity and thickness. MCRT can therefore be used in developing fundamental relationships between a material’s thermal performance and its microstructural building blocks. The major restriction of the MCRT in fibrous media is that it requires the fiber diameter to be large compared to the wavelength of the incoming radiation, so that the rules of geometrical optics can be applied. We have a fast and accurate analytical MCRT simulation method to study radiative heat transfer in fibrous media. |
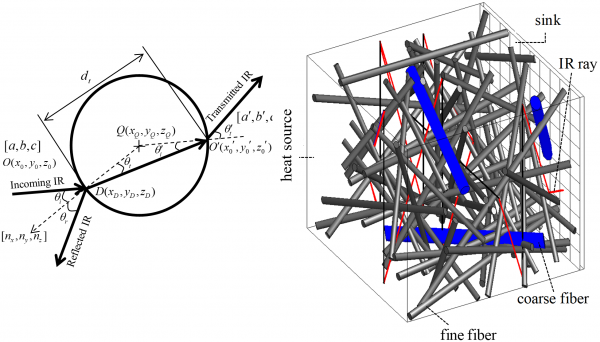 The figure on the left shows the schematic of a ray passing through a fiber. The figure on the right is a visualization of the trajectory of a ray traced through a fibrous media comprised of fibers with different properties for illustration. The ray is shown in red color. Black lines show the ray changing position when periodic boundaries are encountered. Coarse and fine fibers are shown with blue and gray colors, respectively [Arambakam et a., 2012, Tahir et al., 2010]. |
| To simulate radiative heat transfer in media comprised of smaller fibers (e.g., nanofibers) where the principles of geometrical optics do not apply, we developed a dual-scale modeling approach. This computationally-affordable 3-D method was developed to simulate the transfer of radiative heat through fibrous media comprised of fibers with different diameters and 3-D orientations. The simulations started by generating a virtual fibrous material with specified microstructural properties and then by computing the radiative properties of each fiber (i.e., effective phase function, scattering coefficients, and absorption coefficients) in the structure using the Mie Scattering theory. Considering independent scattering formulations, the radiative properties of the insulation material were computed by summing up the radiative properties of each individual fiber, after transforming the phase function values from the fiber’s local 3-D coordinates system to a fixed global coordinates system. These radiative properties were then used in the Radiative Transfer Equation (RTE) equation to compute the attenuation and augmentation of InfraRed rays of energy as they traveled through the media. Using the Discrete Ordinate Method (DOM), the RTE was then discretized into a system of twenty four coupled partial differential equations and solved numerically to obtain the rate of heat transfer through the entire thickness of the media. |
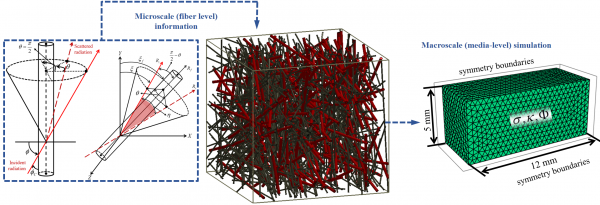
In our dual-scale simulations, microscale (fiber-level) information is used in a macroscale (on scales comparable to the dimensions of the entire media) finite element simulation predict the rate of radiative heat transfer through a fibrous insulation. The figure on the left shows the interactions of an IR ray with a fiber in the fiber’s coordinate system (the way existing equations are reposted in the literature). Since different fibers in a fibrous media (the figure in the middle) have different orientations, the orientations of the fiber, incident IR and scattered IR had to be defined in a global coordinate system before they could be used to estimate the radiative properties (i.e., effective phase function, scattering coefficients, and absorption coefficients) of the insulation medium as a whole (middle figure) and be used in the macroscale (the figure on the right) simulations [Arambakam et al., 2013]. |
| Studying media with different microstructural properties, we quantitatively showed that increasing solid volume fraction, thickness, or fibers’ through-plane orientation increases the rate of heat transfer through insulation. More interestingly, it was discovered that there exists a fiber diameter for which radiation heat transfer through a fibrous media is minimal. |
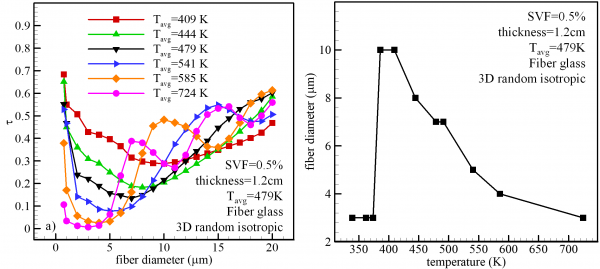
Fibers in these structures are allowed to have 3-D isotropic orientations. It can be seen in the left figure that as fiber diameter increases from 0.75 µm to 20 µm heat transmittance through the media decreases first, but then starts to increase. It can be seen that optimal fiber diameter at which best radiation insulation can be achieved depends on the operating temperature of the media. In other words, smaller fibers are better at insulating radiative heat generated from higher source temperatures, and decreasing the temperature of the source increases the diameter of the fibers that best insulate the heat. The figure on the right shows the optimal fiber diameter as a function of source temperature [Arambakam et al., 2013]. |
| We also developed a methodology to simulate heat transfer in multi-component fibrous insulations (insulations made up of different combinations of fibers with different materials or dimensions). We obtained the resistance of the media to radiative heat using the above dual-scale simulation method and combined it with that obtained analytically for the conduction heat transfer through the media (as in parallel resistors). |
For demonstration purposes, insulation media made up of glass and mineral wools fibers with different mass fractions and fiber diameters were simulated in blended (figures on the left) and layered (figures on the right) configurations and their insulation performance were compared with one another. It was found that layered and blended fibrous multi-component insulations exhibit similar performance. It was also found that the stacking sequence does not affect the thermal resistance of layered media [Arambakam et al., 2014]. |
Representative Publications:
|
Acknowledgement:
|