Structural Modeling of Fibrous Materials
| Our group has recently developed a physics-based model to generate 3-D fibrous geometries that can realistically mimic the microstructure of a fibrous material (e.g., an electrospun media) made of fibers with different degrees of softness. The uniqueness of this model is that it allows for the fibers to deform (based on their measured stiffness) at the fiber–fiber crossovers with no non-physical fiber-fiber interpenetration. The model can accept inputs like fiber diameter distribution, fiber bending properties, initial fiber orientation, and manufacturing conditions. The outputs from the model can include, but are not limited to, porosity, thickness, and final fiber orientation. The fact that porosity, thickness, and final fiber orientation are outputs (rather than being input like the case of all previous nonwoven structure generation models) is another unique attribute of this modeling method. This means that one can potentially simulate how the material is being produced or how the manufacturing conditions can affect its porosity, thickness, or fiber orientation. For instance, consider the electrospinning process. While it is quite easy to set up an electrospinning unit, it is very difficult to predict the outcomes of an electrospinning experiment in terms of fiber diameter, mat thickness, or mat porosity. This is mainly due to the complicated physics of fiber formation in electrospinning and also the minuteness of the resulting fibers. For instance, there is no accurate method of measuring the thickness, and consequently the porosity, of an electrospun fiber mat. This is because such mats are generally very thin, and at the same time, very soft (tend to deform during measurement). In this concern, we have developed a computational tool that allows one to study the effects of electrospinning parameters, such as voltage, needle-to-collector distance (NCD), or polymer concentration, on the thickness and porosity of the resulting fibrous materials. |
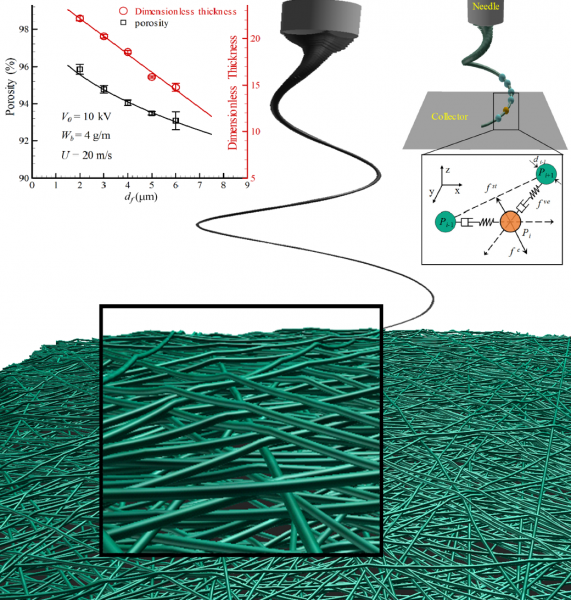 Virtual electrospun polystyrene with a basis weight of 4 g/m^2 and an average fiber diameter of 3 µm. The inset figure on the left shows the effects of fiber diameter on the porosity and dimensionless thickness of the resulting electrospun fibermats [Yousefi et al., 2018]. |
| This modeling approach is based on representing a fiber as an array of beads (mass) connected to one another via spring and dampers (referred to here as mass-spring-damper model). In this method, the time-dependent shape and position of each fiber is obtained by numerically solving a system of coupled ordinary differential equations (e.g., 500 second-order differential equations per fiber). This model can potentially incorporate the manufacturing conditions by which a fibrous material is produced (e.g., melt-blowing vs. wet-laying vs. electrospinning), and how the process parameters can affect its properties. |
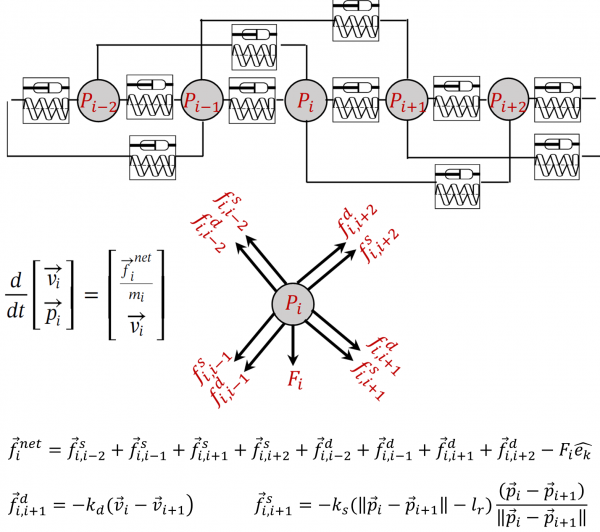  Our Mass-Spring-Damper representation of a fiber is shown. The number of springs and dampers, their configurations, and their properties can be varied to model different polymeric or non-polymeric fibers. A virtual nonwoven having an average fiber diameter of 10 μm, a basis weight of 76 g/m^2, and a porosity of 82% is shown in the figure to the right. Note how the fibers bend at fiber-fiber intersections [Moghadam et al. 2019]. |
| We have also expanded the above model to create a fast and flexible algorithm to simulate the microstructure of loosely deposited particles of arbitrary shapes (e.g., airborne dust particles). Our approach is based on representing a non-spherical particle as an assembly of spherical beads connected to one another via springs and dampers. This model allows one to study the effects of particle shape, particle size, and particle rigidity on the thickness and porosity of the resulting structures. |
 Different examples of virtual dendritic deposits made of soft particles of different 3-D shapes. The figures from left to right show particles with the shape of Jacks toys (3-D star), cubes, and spheriocyliders, respectively [Yousefi and Tafreshi 2020]. |
Representative Publications:
|
Acknowledgement:
|